こんにちは、Яeiです。
今回は早稲田大学大学院(数学)を修了した私が、微分のイメージについて解説していきたいと思います。
恐らく高校2年生で習うであろう微分。数々の生徒を数学の道から振るい落としてきたこの分野を超簡単なイメージで理解できるように解説致します。
なお、ここではイメージを優先しているため厳密性は捨てております。
興味がある方は大学で「微分方程式論」などの微分にまつわる学問を勉強してみて下さい。
大学で専門的に学ぶと、編微分方程式などの分野に派生していき、ゆくゆくは「自然現象を数式で表す」といったとても楽しい学問へと変わります。
こうした学問を学ぶ上での基礎的な知識となりますので、是非ここでイメージだけでも身につけていって下さい。
目次
微分のイメージ
結論(微分は「傾き」)
- 微分のイメージは「傾き」です。
これだけ分かっていればもう大丈夫です。
「え?何言ってるのこの人」と思われるかもしれませんが、本当にこのイメージだけで「微分」という概念の理解は事足ります。
しかし「そんなこと言っても、こんな簡単な概念は忘れようがないよ」と思われるかもしれませんが、高校では問題を解くことに夢中でこのイメージが抜け落ちている方が多いのです。
スピード勝負の受験勉強の弊害とも言えましょうか。
ですが、当然ではありますが問題を解く際もこの「傾き」イメージがあれば「なるほど」となる問題も多々あります。
それではもう少し詳細に説明していきたいと思います。
傾きとはそもそも何か
「傾きとは何か」は中学生時代に既に学んでおります。
一般的に「机が傾いている」とか「この坂道傾きが急だよ」とかで使うあの傾きのことです。
数学では以下のように考えます。
$$ (直線の傾き)=\frac{yの増加量}{xの増加量} $$
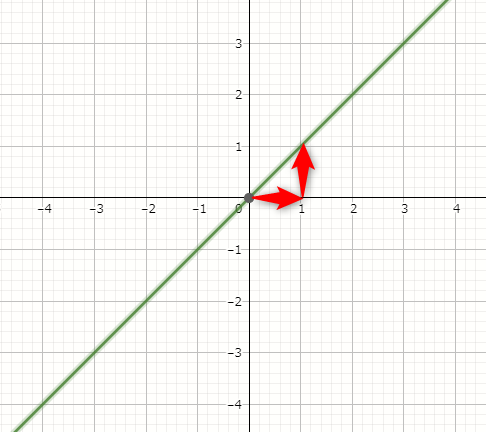
少し小難しいかもしれませんが「x方向に1進むとy方向に1進む」場合は、
$$ (直線の傾き)=\frac{1}{1}=1 $$
となります。「増加量」と聞くと難しいかもしれませんが、どれだけ「x方向に1進んだ場合にy方向にどれだけ進んだか」となります。
そして、このとき傾きは1となります。
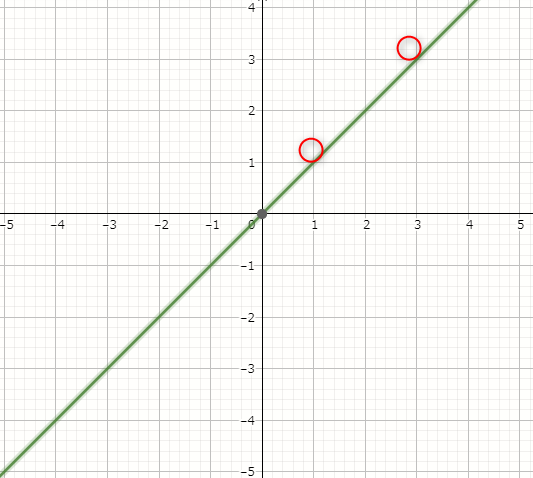
ここで注目してもらいたいのは「どの地点xであっても傾きは変わらない」という点になります。
x=1の地点にいる人と、x=3の地点にいる人では傾きは1で変わりません。
(仮に、x=3の地点にいる人が「俺のいるところの方が坂の傾きが急だよ!」と言ったとしてもそれは気のせいです)
ここまではまだ中学レベルの「傾き」の復習でした。
曲線の傾き
次に曲線の傾きについて見ていきましょう。
例えば次のような曲線を考えたとき、x=0の地点にいる人は「傾いていないよ」となるはずです。
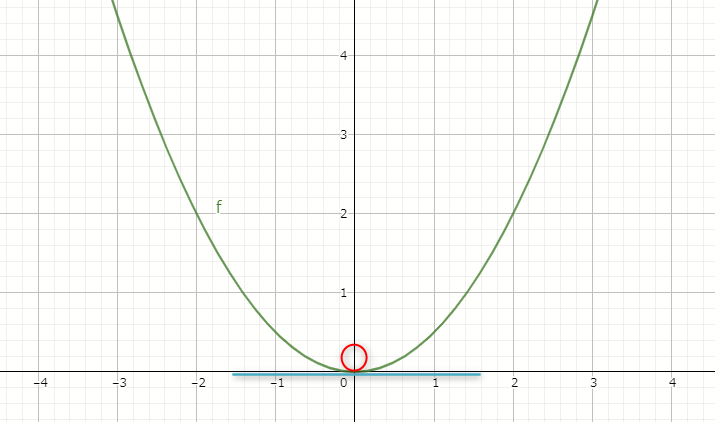
これに対して、x=2の地点にいる人は「いやぁ、結構な急坂だよ」となると思います。
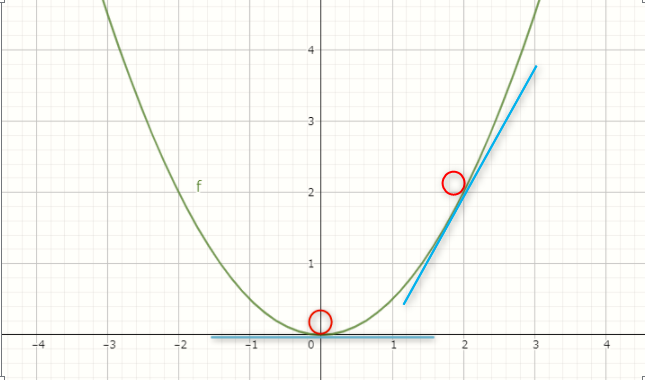
x=4の地点にいる人にいたってはもはやロッククライミングレベルで傾いていると感じるのではないでしょうか。
では、この曲線の「傾きは?」と聞かれた際になんと答えればよいのでしょうか。
直線の場合はどの地点でも傾きは一緒だったのでビシッと傾きを答えることが出来ましたが、曲線の場合は場所によって傾きが異なります。
そこで登場するのが「微分」という概念になるのです。
微分の発想
さて、曲線の傾きを求めるための解決作として「微分」を考えていきましょう。
曲線の傾きをビシッと答えられない理由は「地点によって傾きが異なる」ことにありました。
つまり、自分がいる地点の情報を渡してあげることでその地点における傾きを答えてくれる「関数」が用意できれば曲線の傾きはある意味求まったようなものですよね。
※ 関数が分からない方は一緒に以下の記事も見てみて下さい。
この関数を作る技が「微分」となります。そして作った関数を特に「導関数」なんて呼んだりします。
先ほどの例のグラフを微分すると「自分の地点情報を渡してあげるとその地点における傾きを求める」すごい関数が出来上がるわけです。
x=1の地点にいる人が「x=1」といった情報を渡してあげると、関数は「これくらい傾いてますよ」と結果を返してくれるのです。
微分のイメージは傾きですが、もう少し正確に例えると「傾きを求めるための関数を作る必殺技」といったところでしょうか。
ここまでのイメージがあれば微分の分野はもう怖くはありません!
微分の定義を考える

微分って名前がそもそも難しいですよね。微って文字は「微量」とかで使われており「わずか」というイメージがあります。
「傾きを求めるための関数を作る必殺技」のどこら辺に「微量」な要素があるのでしょうか。
ここで、もう一度思い出して下さい。微分のイメージは「傾き」です。
このイメージを常に頭に入れつつ、曲線の場合であっても無理矢理傾きを求めてみましょう。
具体的に$x=2$の地点の傾きを求めて見ましょう。
まずやることとして$x=2$の地点を、それはもうめちゃくちゃ拡大してみましょう。
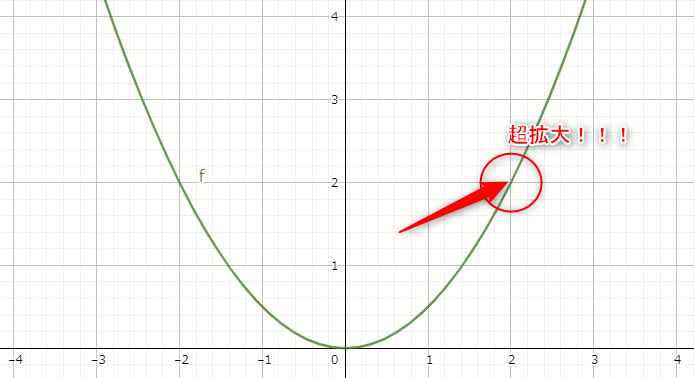
すると以下のようになります。
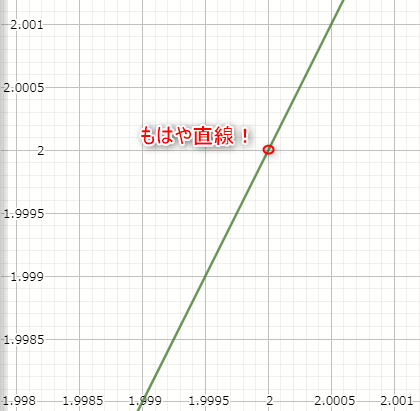
これはツールの限界まで拡大してみたのですが、
一点に焦点をあてて拡大すると、もはや直線のようになっていることが分かると思います。
これをもっともーーーっと拡大していくと「もうこれ直線でいいんじゃね?」というレベルまでになります。
これが極限の考え方となります(機会があれば極限についても記事にしたいと思います)。
そして、ここが「微」を表している所以にもなってくるわけです。
直線であれば、中学時代に傾きの求め方を習いましたよね?
$$ (直線の傾き)=\frac{yの増加量}{xの増加量} $$
で求められるのです。この発想が微分の定義の発想となります。
それでは微分の定義を掘り下げていきましょう。
曲線の式を
$$y=f(x)$$
とします(例えば$x=1$の地点の人の$y$の値は$f(1)$となります)。
そして、先ほどのめちゃくちゃ拡大したグラフに対して以下のように$x=a、x=b$地点を考えます。
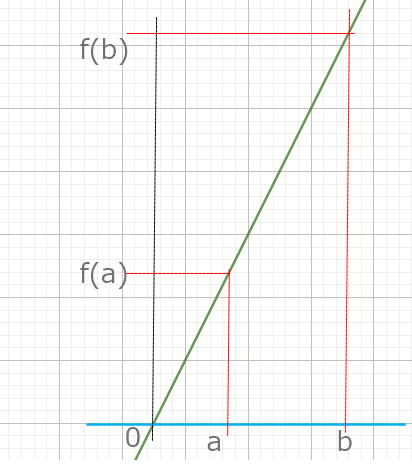
すると、中学生時代に学んだ傾きの求め方より、
$$ (直線の傾き)=\frac{yの増加量}{xの増加量} =\frac{f(b)-f(a)}{b-a} $$
となります。
しかし思い出して下さい。この傾きってめちゃくちゃ拡大した際の傾きになりましたよね。
つまり、この式が成り立つのは「aとbがめちゃくちゃ近い」とき限定になります。
「aとbがめちゃくちゃ近い」ことを数学記号を用いて表現すると以下の式になります。
$$ (曲線のx=aにおける傾き)=\displaystyle \lim_{ b \to a } \frac{f(b)-f(a)}{b-a} $$
ここで$\displaystyle \lim_{ b \to a }$が「aとbがめちゃくちゃ近い」という意味になります(厳密性を捨ててます)。
さらっと出てきたこの式こそが「微分の定義」となります。
ちなみに、左辺の「$(曲線のx=aにおける傾き)$」は長くてかっこ悪いので、
$$ f'(a)=\displaystyle \lim_{ b \to a } \frac{f(b)-f(a)}{b-a} $$
と表します。$f'(a)$の「$’$」が微分マークになるのです。
このように微分のイメージは「傾き」となり、微分の定義もこのイメージ通りになっていることが分かりました。
念のため$f(x)=x^2$レベルの微分だけでも見ておきましょう。
$x=a$地点における微分は、
$$\begin{split} f'(a)=\displaystyle \lim_{ b \to a } \frac{f(b)-f(a)}{b-a}&= \displaystyle \lim_{ b \to a } \frac{b^2-a^2}{b-a} \\
&=\displaystyle \lim_{ b \to a } \frac{(b+a)(b-a)}{b-a} \\
&=\displaystyle \lim_{ b \to a } (b+a) \\
&=2a \end{split} $$
のようになります。あとは$a$に具体的な値を入れれば$y=x^2$の傾きは誰でも求められるようになったのです。
ここで重要なのは「微分の定義を忘れてしまっても、イメージからすぐに定義を導き出せる」ということです。
高校時代、丸暗記していた人にとって「定義を忘れた!」「公式を忘れた!」ということは致命傷になります。
しかし、このようにイメージを覚えておくだけで定義も導き出せますし応用問題も解けるようになってきます。
もちろん、「問題を解く力」に関しては本人の努力次第になりますが、まずはイメージをしっかりと持っておきましょう!
微分ができると嬉しいこと

ところで「微分で傾きを求めて何が嬉しいの?」という疑問もあるかと思います。
普通に解析するのに嬉しかったりもするのですが、ここでは少しだけ馴染み深い例でを挙げてみようと思います。
数学では「自然現象はすべて数式で表せる」と言われております(もちろん実用性がないなどの問題はありますが)。
インフルエンザの流行モデルとか、コーヒーの冷め方とか、外来種がどのくらいの速度で繁殖していくかとか。
これらはすべて数式で表すことができるのです。
2020年、2021年は新型コロナウイルスが流行しました。
こうしたウイルスのパンデミックモデルも恐らく出来てくると思います(感染症の流行モデルはすでに様々な研究がされております)。
その場合、その数式を微分してみると傾きを求める関数が作れます。
ここで、例えば2021年8月情報を関数に渡してあげると傾きを求めてくれるのですが、この傾きが急であれば「この先も爆発的に感染が広がる」と予想できます。
あるいは傾きが0に近い場合は「流行は今がピーク」と予想できます。
このように、微分を用いるとある時点において将来を予想できたりするのです。
小難しい数式が出てこなければ、数学って結構面白いとは思いませんか?
当記事は以上となります。
高校数学の数学の微分で振るい落とされた方は、このイメージをもって再度子供と一緒に勉強するなりしてみて下さい。
案外「なんだ、こんなものか」となるかもしれませんよ。
長々とお疲れさまでした!
次回、積分については以下をご参照下さい。

